1. 동적계획법이란
큰 문제를 더 작은 문제로 분해해 각각의 결과를 저장하여 본래 문제를 해결하는 알고리즘 설계법이다.
- 문제의 입력 instance를 더 작은 부분 instance로 나눈다.
- 작은 instance를 먼저 해결하고 그 결과 저장한다
- 저장된 결과들로 큰 instance를 해결한다.
이를 주로 Bottom-up, 상향식 방식으로 진행하게 된다.
코딩테스트에서 주로 숫자 제한범위가 크고, 경우의 수가 방대한 문제가 주로 DP로 설계하면 해결된다(고 함)
2. Memoization
n번째 피보나치 수열의 수를 구하는 문제를 재귀식으로 풀 때를 생각해보자.
func fibonacci(n)
if n < 2
n
else
fibonacci(n - 1) + fibonacci(n - 2)
보다시피 f(n) = f(n-1) + f(n-2)이므로, f(n)을 해결하기 위해 f(n-1)과 f(n-2)를 호출하는 하향식 방법이다.

또한 f(5) = f(4) + f(3), f(6) = f(5) + f(4) 에서 f(4)가 중복 사용되는 것 처럼,
동일한 문제가 중복 계산되어 효율이 떨어질 수 있다.
DP에서는 이러한 중복계산을 방지하도록 배열과 같은 메모리 공간에 하위 문제의 계산결과를 저장하여
필요할 때 이를 다시 호출하여 사용한다.
이를 Memoization 이라고 부른다.
3. DP의 조건
그럼 모든 재귀를 DP로 풀면 더 효율적인거 아니야? 라고 할 수 있으나
DP로 풀 수 있는 조건이 있다.
A. 중복되는 부분 문제 (Overlapping Subproblems)
위의 피보나치 수열의 경우 처럼 부분 문제를 계산하는데 중복계산이 발생하는 경우에
DP를 적용하여 효율적인 알고리즘을 설계할 수 있다.
DP는 나누어진 문제의 결과값을 저장하여 재사용하는 것이 중요하기 때문이다.
B. 최적 부분 구조(Optimal Substructure)
부분 문제를 최적 결과 값으로 상위 문제의 최적 결과를 낼 수 있어야 한다.
무슨 소리냐 하면,

위의 그림에서 A->D로 가는 최단 경로를 찾아보자.
A에서 B를 가는 최단경로, A에서 C로 가는 최단경로를 결정하고
그 경로들을 이용해 A->D까지의 최단경로를 찾을 수 있다.
이처럼 하위문제의 최적해가 상위문제의 최적해에 이용되는 것이다.
4. DP로 문제를 해결하기
DP로 문제를 해결하는데 중요한 두가지가 있다.
A. 변수간 관계식
고등학교 때 자주 접한 점화식이다.
피보나치 수열은 f(n) = f(n-1)+f(n-2) 으로 관계식을 세울 수 있다.
이항계수 문제의 경우
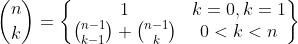
로 나타낼 수 있다.
이처럼 큰 문제를 작은 문제로 분해하여 이들간에 관계식을 세워야 한다.
B. Memoization
하위 문제들의 결과를 저장할 배열과 같은 메모리 공간을 생성하고,
이 공간에 값을 저장하여 이후 호출해 재활용해야한다.
이를 마쳤으면, 최하위 문제부터 차례대로 계산하여 가장 큰 문제를 해결하도록 구현하면 된다.
가장 하위의 부분 문제의 결과값은 할 수 있다면 미리 지정한다.
5. 구현
구현에는 두 가지 방법이 있다. 피보나치 수열을 예로 살펴보자.
A. Bottom-up, 상향식
이는 반복문을 사용하여 구현한다.
가장 작은 문제부터 해결하여 이들의 최적해를 배열에 저장하고, 차차 상위문제를 해결해나간다.
의사코드로 확인하자.
int dp[n]
// 최하위 부분문제의 초기값 지정
dp[0] = 0
dp[1] = 1
func fibo(n) {
for i in 3...n {
dp[i] = dp[i-1] + dp[i-1] // 배열에서 재활용
}
return dp[n]
}
B. Top-down, 하향식
재귀식으로 구현한다.
int dp[n]
dp[0] = 0
dp[1] = 1
func fibo(n) {
if(dp[n] != 0) // 배열에 저장된 값이 있다면 재활용
return dp[n]
dp[n] = fibo(n-1) + fibo(n-2)
return dp[n]
}
6. 예제: 이항계수
고등학교 수학에서 배운 다항식의 정리에 대한 식, 이항정리 문제이다.
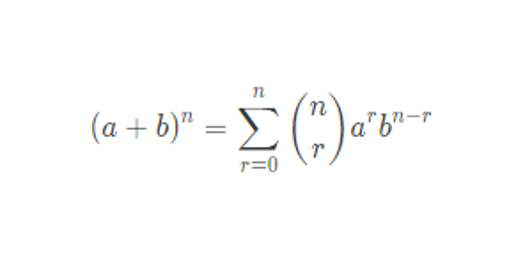
이 식에서 계수만 따오면 이항계수이다.
수학시간은 아니므로 적당히 넘어가고
우리는 이 계수, 주어진 n과 k에 대한 계수 (n,k) 가 몇인가를 알고싶다.
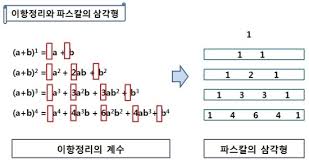
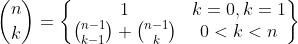
A. 재귀
func bin(int n, int k){
if(k == 0 or n == k)
return 1
else
return bin(n-1,k-1) + bin(n-1,k)
}
간단하다. 위에서 세운 관계식을 그대로 구현하면 된다.
시간복잡도는 T(n,k) = T(n-1,k-1) + T(n-1,k) ≈ 2(n! / k!(n-k)!) 로 대강 엄청나다.
이를 단순재귀로 풀면 바보라 보면 되겠다.
B. DP
DP는 일단 배열이 필요하다. 2차원 배열 B[i][j] 은
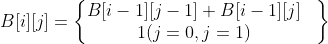
이라고 하자.
그리고 계수를 나타내는 파스칼 삼각형을
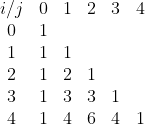
이처럼 보았을 때 1이 아닌 값들은
좌표 (i-1,j-1)의 값과 (i-1,j)의 합과 같다.
2차원 배열 B[i][j]를 위의 그림같이 사용한다면 우리는 DP로 구현할 수 있을 것 같다.
n과 k가 주어졌을때 n번째 행의 k번째 수를 찾는 DP로 구현한 의사코드이다.
pascal[100][100] = {0, } // 계수를 저장할 이차원배열, 모두 0 초기화
func bin(int n, int k){
for (i in 0...n)
pascal[i][0] = 1 // 삼각형의 좌측 변은 모두 1로 고정
for (i in 1...n) {
for j in 1...i {
if (j >= k) continue // k 값 이상으로는 구할 필요 X
pascal[i][j] = pascal[i-1][j-1] + pascal[i-1][j]
}
}
return pascal[n-1][k-1]
}
시간복잡도는 다음과 같다.
n과 k가 주어졌을때 i값에 따라 for j의 루프가 몇 번 실행되는지 따져봐야한다.
i = 0 일때 1번,
i = 1 일때 2번,
i = 2 일때 3번 ...
i = k 일때 k + 1번
i = k + 1일때 k + 1번 ...
i = n 일때 k + 1번
따라서 루프는 1 + 2 + 3 + ... + k + (k+1) * (n-k+1) 번
= k(k+1)/2 + (k+1)(n-k+1) = (2n-k+2)(k+1)/2
≈ Θ(nk)
'개발 > 알고리즘' 카테고리의 다른 글
| 누적합 (0) | 2024.06.16 |
|---|---|
| 최장 증가 부분 수열, LIS 알고리즘 (0) | 2024.05.14 |
| c++) 백준 14888 백트래킹, 연산자 끼워넣기 (0) | 2024.03.25 |
| 백트래킹(Backtracking) 알고리즘 (1) | 2024.03.24 |
| c++ 하노이의 탑, 재귀함수, 백준 11729 (2) | 2024.03.22 |
